Introduction

Are you struggling to calculate the enigmatic area concealed beneath an alluring curve? Look no further than the realm of Microsoft Excel, where mathematical sorcery transforms intricate integrals into effortlessly attainable values. Excel empowers you with an array of versatile tools, granting you the power to conquer this enigmatic domain and unlock the secrets it holds.

Image: webgiasi.vn

Embark on an enlightening journey as we decipher the mysteries of finding the area under a curve in Excel, a skill that unlocks boundless possibilities in the realms of science, engineering, finance, and beyond. Prepare to unveil the hidden treasures beneath the surface of complex functions, as we empower you with the knowledge to master this enchanting art.

Laying the Foundation: Understanding the Concept of Integrals

To fully grasp the essence of finding the area under a curve, we must delve into the enigmatic realm of calculus, where integrals reign supreme. These mathematical marvels provide a transformative lens through which complex curves are rendered as simple figures, revealing the hidden areas they encompass.

Imagine a captivating curve gracing the world of Cartesian coordinates, gracefully connecting a myriad of points. The area beneath this captivating masterpiece represents a quantity that integral calculus empowers us to calculate with precision.

Conquering the Integrals: Unveiling the Power of Excel

Excel, the formidable spreadsheet software, harbors an arsenal of functions that empowers you to wield the power of integrals. Prepare to witness the transformation of complex equations into manageable computations, as we unveil the secrets of this computational marvel.

1. **The Integral Function: A Gateway to Infinite Possibilities**
– The Integral function, symbolized by INTEGRAL, stands as the cornerstone of our quest. This formidable tool allows you to evaluate definite integrals, revealing the area beneath a curve with pinpoint accuracy.
– To invoke the Integral function’s powers, simply follow this syntax: =INTEGRAL(lower_limit, upper_limit, function_to_integrate, [variable]), where each parameter plays a pivotal role.

2. Breaking Down the Integral’s Components:
– **lower_limit:** This parameter signifies the lower boundary of the integral, marking the starting point of our journey along the curve’s enchanting path.
– **upper_limit:** The upper boundary awaits at the other end of the spectrum, marking the end of our integral adventure.
– **function_to_integrate:** This entity represents the enigmatic curve itself, whose secrets we seek to unveil.
– **variable:** The variable parameter, often denoted by x or y, embodies the independent variable that breathes life into the function.

A Glimpse into the Diverse Applications: Unlocking the Power of Area Calculations

The art of finding the area under a curve extends far beyond theoretical realms, permeating countless practical applications across a kaleidoscope of disciplines. From unraveling the mysteries of physics to guiding financial decisions, this technique unveils boundless opportunities for exploration.

1. **Delving into the Realm of Physics**
– In the world of physics, mastering the area under a curve empowers you to probe the ethereal realm of kinematics, unraveling the intricate dance of objects in motion.
– By calculating the area beneath a velocity-time graph, you gain the power to uncover the total displacement of an object over a given time frame.

2. **Illuminating the Path of Economics**
– The enigmatic area under a curve holds profound significance in the world of economics, offering insights into consumer behavior and market trends.
– Calculating the area beneath a demand curve empowers you to determine the total revenue generated at various price points.

Refining Your Craft: Tips and Tricks for Excel Mastery

To elevate your Excel prowess and emerge as an unparalleled master of area calculations, heed these invaluable tips and tricks:

1. **Embrace the Power of Graphing**
– Visualizing the curve before embarking on the integral journey can illuminate potential pitfalls and provide invaluable insights.
– Utilize Excel’s graphing capabilities to paint a vivid picture of the function, revealing its intricate contours and guiding your analytical approach.

2. **Leveraging Numerical Techniques**
– In certain scenarios, numerical integration techniques, such as the Trapezoidal Rule or Simpson’s Rule, can provide approximate solutions when analytical methods prove elusive.
– These techniques subdivide the area into manageable trapezoids or parabolas, revealing the hidden secrets of the curve’s embrace.

Conclusion

As the curtains fall on this captivating discourse, we have embarked on an enlightening journey, unearthing the secrets of finding the area under a curve in the enigmatic realm of Excel. Through our exploration of integrals and their practical applications, we have equipped you with the tools to unravel the mysteries of complex functions and quantify their hidden depths.

May this newfound knowledge ignite a passion for further exploration, as you continue to master the art of area calculations in Excel. Remember, the path to mastery is paved with curiosity, perseverance, and a relentless pursuit of knowledge. As you delve deeper into this enchanting realm,

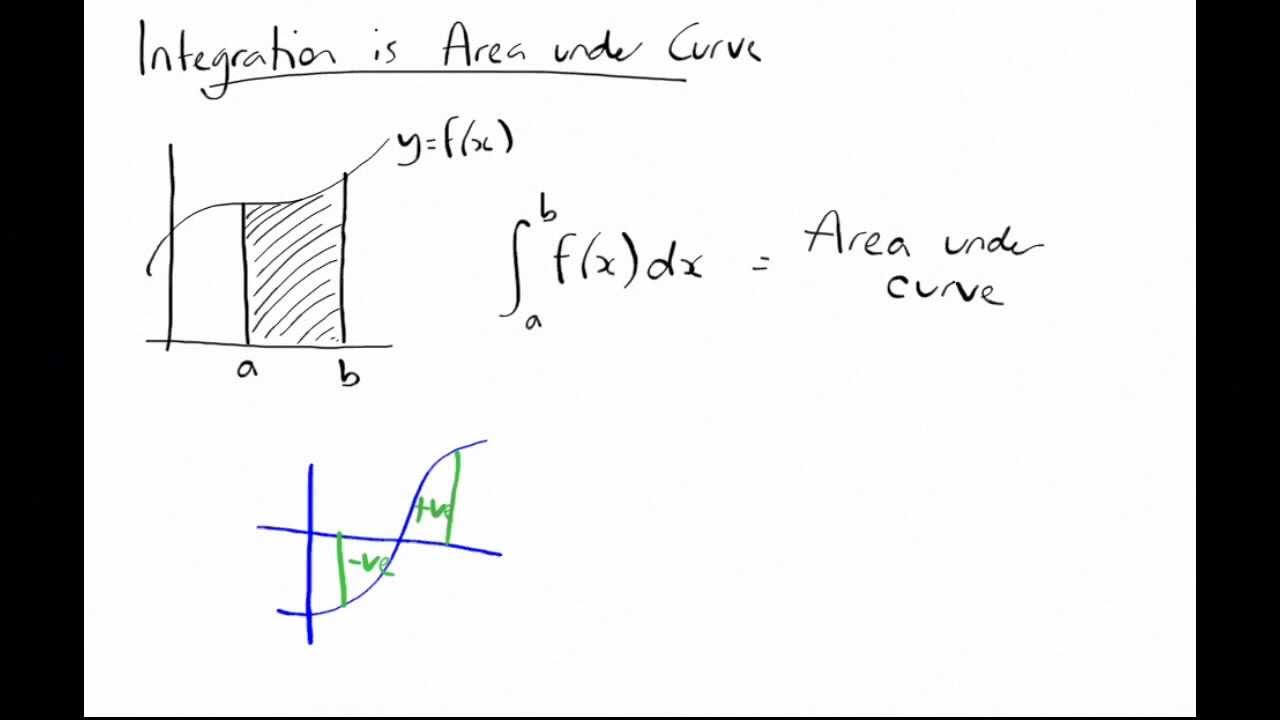
Image: haipernews.com

How To Find The Area Under A Curve In Excel